Angle Computations from quaternions : Sandwich Product

In order to transform quaternion into a point’s movement and rotation we can use transformation called Sandwich Product

The quaternion in terms of axis-angle is:

$$q = cos(a/2) + i ( x * sin(a/2)) + j (y * sin(a/2)) + k ( z * sin(a/2))$$

where:
a=angle of rotation.
x,y,z = vector representing axis of rotation.
i,j,k = represents 3 imaginary dimensions.

Quaternions have 4 dimensions; one real dimension and 3 imaginary dimensions(i,j,k). Each of these imaginary dimensions has a unit value of the square root of -1 (but they are different square roots of -1):

$i^2 = j^2 = k^2 = -1$
$ij = k, ji = -k$
$jk = i, kj = -i$
$ki = j, ik = -j$

The formula for 3D rotation(Sandwich Product)can be represented as:

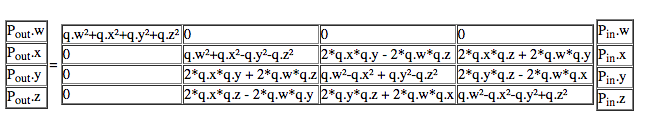
Double multiplication ‘i’ now represents a 90° for each multiplication, that is, 90°+90°=180° and similarly for ‘j’ and ‘k’.

Note also that the q.w²+q.x²+q.y²+q.z² in the top left element represents the scaling factor. For pure rotation, we divide everything by:

$$1/ (q.w^2+q.x^2+q.y^2+q.z^2)$$

so that $P_{out}.w = 1$

Referred from Euclideanspace.com

How to use the sandwich transfomation matrix

For instance, if you have quaternion from IMU sensor and you want to know the gravitational component in terms of x axis and y axis ($g_x$, $g_y$ respectively), the expressions would be:

$g_x = 2q_xq_z - 2q_wq_y$
$g_y = 2q_yq_z + 2q_wq_x$

---

• Algorithms/IMU (2)